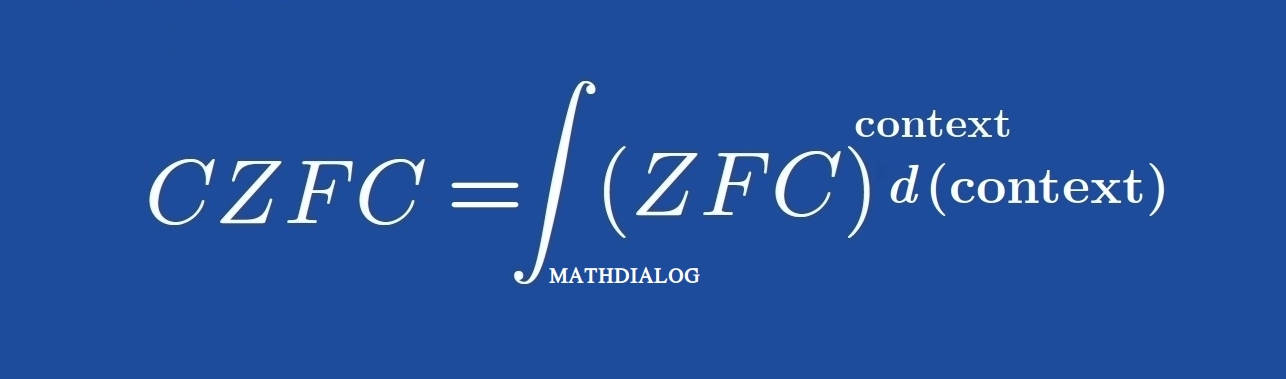
In the realm of mathematics, where abstract concepts often challenge intuition, tools that enhance comprehension are invaluable. Mathdialog emerges as a pioneering platform dedicated to transforming the often opaque world of formal mathematics into an accessible, engaging experience. At its core, Mathdialog addresses a fundamental tension in mathematics education: while formal verification ensures the rigor of proofs, it frequently leaves learners grappling with the "why" behind the logic. By integrating interactive elements, Mathdialog redefines how we engage with mathematical proof, making it not just a static document but a dynamic, interactive exploration.
The platform's foundation lies in set theory, the de facto standard foundation for modern mathematics. Mathdialog's "NUCLEUS"—a collection of about 100 essential definitions and theorems that constitutes its starting point—has theorems like binary unions properties (e.g., BIN_UNION_P01 and BIN_UNION_P05), the non-emptiness of sets (NOEMP_P01), and the existence of Cartesian products (CART_PROD_EXIST). Elements as these, forms a special version of ZFC set theory, providing a minimal yet robust scaffold for exploring more complex structures. Users can dive into definitions such as FUNC (functions), INFIMUM, or MAXIMAL (infimum or maximal elements of a set), each linked seamlessly to theorems that demonstrate their application. This structure not only exemplifies easy formal proof construction but also serves as a gateway for learning formal math in a structured manner.
Central to Mathdialog's innovation is the automatic building of Formal proof explainers. Traditional theorem prover systems, like Lean or Rocq (formerly Coq), excel at formal verification—mechanically checking the validity of a mathematical proof through exhaustive logical steps. However, they often output raw "source code" not natural to human readers. Mathdialog flips this paradigm by acting as a proof assistant that goes beyond verification. Once a proof is verified via its computer proof checker (human-to-machine proof in Mathdialog terminology), the platform transforms it into an interactive dialogue (a machine-to-human proof). Imagine querying a proof mid-exploration: "What is the definition of this term?" or "Where does this hypothesis come from?" Mathdialog allows users to get instant responses, tracing lineages back to axioms or prior theorems, such as linking a hypothesis in GROUP_P04 to the uniqueness of inverses in INV_GROUP_UNIQUENESS.
This interactivity is particularly valuable for how to understand proofs. In undergraduate mathematics education, students frequently encounter a "verification gap"—they can follow mathematical proof steps superficially but struggle to internalize the reasoning. Mathdialog counters this with formal proof visualization, rendering proofs as navigable trees or flows where each node expands on demand. For instance, exploring EMPTY_P01 (an empty set's property) reveals not just the logical deductions but the pedagogical rationale: why this step justifies the next, and how it connects to broader set theory implications. Such features align with proof pedagogy, emphasizing explanation over mere computation, and make math proof examples feel alive rather than like a static document.
For those embarking on how to write math proofs, Mathdialog offers practical scaffolding. Beginners can start with entries like KURATOWSKI_PAIR, which formalizes ordered pairs in set theory, and build outward. The platform encourages experimentation: users "build" proofs by querying and refining steps, guided by the system's responses. This mirrors the iterative process of proof-writing—hypothesize, justify, verify—while leveraging a proof checker (human-to-machine proof) to catch errors in real-time. It's akin to having a tireless tutor who specializes in logic education, breaking down barriers between informal intuition and formal mathematics.
Mathdialog's emphasis on interactivity extends to interactive math learning as a whole. Unlike passive textbooks or video lectures, it fosters active engagement, ideal for self-paced undergraduate mathematics education. Consider a student puzzled by INDUCTIVE definitions or FUNC_IN_TO mappings; Mathdialog doesn't just define them—it contextualizes them within live proofs, answering "What is the justification for this step?" with precise, traceable evidence. This approach democratizes access to advanced topics, turning proof pedagogy into an exploratory adventure rather than a rote exercise.
Delving deeper, the platform's technical backbone hints at its potential as a theorem prover companion. While not explicitly tied to one specific system (apart from ZFC), its nucleus of verified statements suggests compatibility with environments focused on formal verification. Proofs like GROUP_P01 (a group property) or LOW_BOUND (lower bounds) are pre-verified, allowing users to focus on interpretation rather than implementation. For educators, this means curating custom "dialogues" around math proof examples, such as dissecting the steps in CART_PROD_EXIST to illustrate existential quantification in set theory.
A standout aspect is how Mathdialog supports how to write math proofs through guided inquiry. Users aren't dumped into a blank canvas; instead, they start with a theorem and peel back layers. For example, querying BIN_UNION_P05 might reveal: "This hypothesis stems from the associative property, justified by EMPTY_P01, which states..." Such revelations build confidence, making easy formal proof development feasible even for novices. It's a subtle shift in mathematics education: from memorizing proofs to conversing with them.
As for resources, mathdialog.com keeps things streamlined—click 'Start Mathdialog' on the homepage to launch the program, where recommended theorems and definitions await. For now, the interactive core suffices, offering over 100 math proof examples that span from basic set operations to group theory essentials.
In essence, Mathdialog isn't just a website; it's a catalyst for rethinking proof explainer tools in the digital age. By prioritizing how to understand proofs alongside formal verification, it bridges the gap between machine precision and human insight. Whether you're a student tackling undergraduate mathematics education, a researcher refining formal mathematics, or an educator seeking innovative interactive math learning aids, Mathdialog invites you to dialogue with math itself. Visit mathdialog.com, select a theorem like NOEMP_P01, and ask away—discover how a simple query can illuminate the elegance of a mathematical proof. In doing so, you'll not only verify logic but truly grasp it, one interactive step at a time.
Copyright 2025 by Carlos E. Freites
Legal stuff