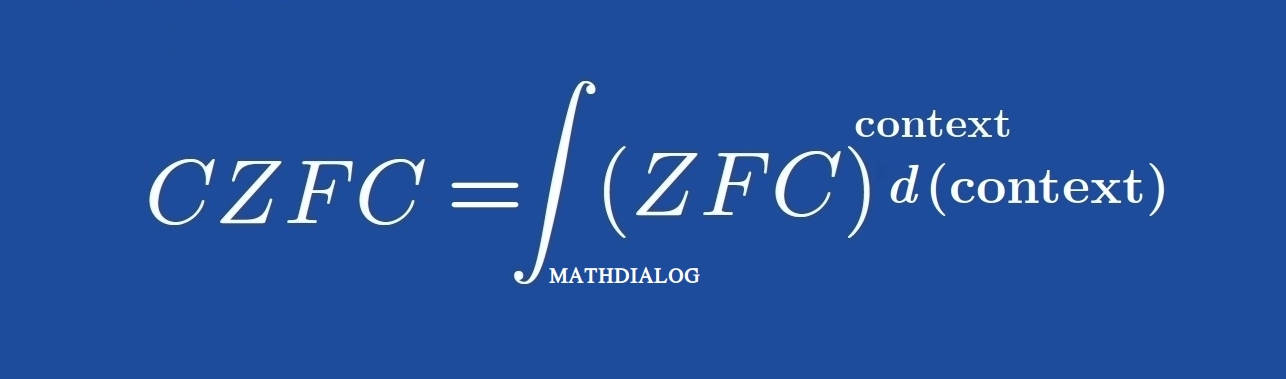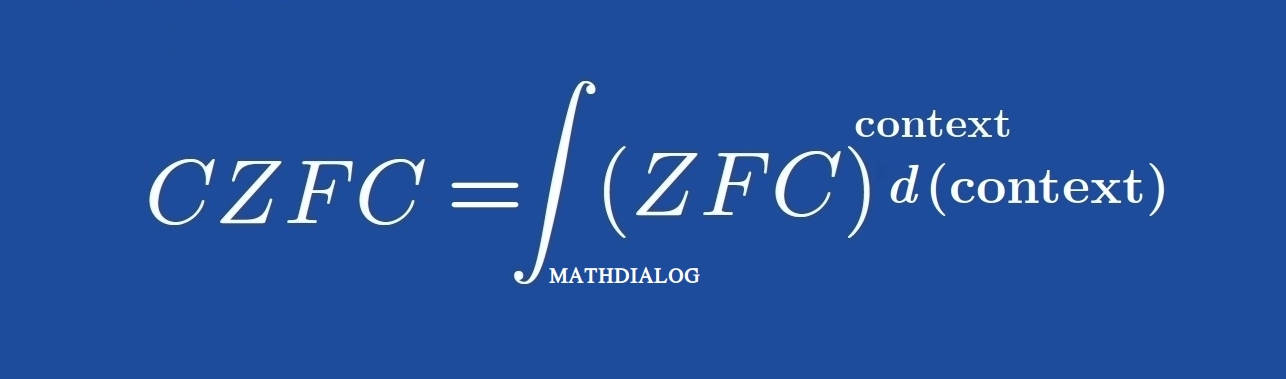CZFC is a version of ZFC with intrinsic context handling. This makes it easy for both machines and humans when dealing with formal proofs. Mathdialog is a computer implementation of CZFC set theory.

In Mathdialog, there are two types of proofs: human-to-machine proofs and machine-to-human proofs. The first type helps users find the CZFC proof (see The Interesting and Fun Game of Mathdialog Proofs). The second is an interactive hypertext environment that helps other users understand the proof in natural mathematical language; that is, users don't need to know CZFC or Mathdialog to understand it.

Logic-commands are the building blocks of proofs. In human-to-machine proofs, they generate new hypotheses and/or goals. A logic-command execute a step in a proof that models a step in books, such as a proof by contradiction, bringing in a definition, or instantiating a quantified formula, etc. For example, if the current goal is: SUBSET(A,B) ==> BG(x,B) then the logic-command IF_RED[] places BG(x,B) as a new goal and SUBSET(A,B) as a new hypothesis.

There are no inference rules in Mathdialog; deductions are done through logic-commands. All logic-commands are described in the Logic-commands Reference Guide.

A proof in CZFC is a list or sequence of logic-commands. All logic-commands are explained in the Logic-commands Reference Guide.

A human-to-machine proof is a dialog between humans and machines that helps the former find a CZFC proof. This dialog takes place in the mathdialog.com web GUI that enables users to send sentences to Mathdialog and get a response from it. The proof starts when the user writes and sends a theorem (one of the kinds of sentences Mathdialog understands) in the command window. It responds by displaying the theorem hypotheses and its thesis on the blackboard, the latter being the proof's main goal. Then, the user writes and sends logic-commands (another kind of sentence Mathdialog understands) one by one until Mathdialog responds with a hypothesis that matches the main goal.

A machine-to-human proof is a hypertext interactive environment where almost all necessary facts to understand the proof are at the user's fingertips. You do not have to know CZFC or Mathdialog to understand them.

To write theorems and some definitions, you have to follow the following syntax depending on the type of object you want to write. In what follows: LABEL is a string with no blank spaces, the theorem or definition name. LFA is a List of Atomic Formulas; they are the theorem or definition hypotheses for humans and the theorem local context for Mathdialog. FORMULA is a logical formula. VAR_LIST is the list of variables in its respective LFA. For example, the informal syntax for theorems is: THEOR[LABEL;LFA;FORMULA] Notice that in Mathdialog, even the most insignificant theorem (there are no corollaries, lemmas, etc.) has a name and one or more hypotheses. A formula alone does not make sense in Mathdialog; it must have a context. In theorems and, as we will see next, definitions, LFA has this functionality. For predicates, the informal syntax is: DEF_PRED[LABEL;LFA;LABEL(VAR_LIST) <==> FORMULA] For comprehension sets, the informal syntax is: DEF_OBC[LABEL;LFA;LABEL(VAR_LIST) = {BG(x,TERM):FORMULA} Suppose TH_EX_UN is the name (label) of a theorem of existence and uniqueness; then the informal syntax for an existential object is: DEF_OBE[LABEL;LFA;LABEL(VAR_LIST) = TH_EX_UN] In Mathdialog, this definition and the theorem TH_EX_UN must be seen as one object (even though a theorem of existence and uniqueness can exist without an existential object definition). In particular, the LFA of the theorem TH_EX_UN and the LFA of this definition must literally match.

A machine-to-human proof is an interactive environment where you control the flow of steps and it helps you resolve your doubts about that proof. When you read a proof in a book and you don't understand a step or where a hypothesis comes from, you have to wait to ask your teacher. Instead, in a machine-to-human proof, you have all the facts to understand it at your fingertips.

You don't have to. Everyone can consult machine-to-human proofs. However, if you want to formulate a new definition or a new theorem to start human-to-machine proofs, you have to be logged in. One of the incentives to prove theorems in Mathdialog is that your name will be associated with that theorem; the more important the theorem you prove, the greater prestige you will have. At the present stage, all theorems are elementary. Their importance depends on the development one is making at a given time. When a logged user consults a machine-to-human proof, the corresponding human-to-machine proof is displayed in a floating window, which is useful to learn about how to make human-to-machine proofs.

There are two types of windows: one is the background fixed windows. In the human-to-machine proofs, they are the blackboard and the command window; in the machine-to-human proofs, they are the goal, the hypotheses, and the step windows. The other type of windows are the floating windows. You can resize them by dragging the lower right corner; you can also move them by dragging their title bar.

That cannot be done. You have to choose a list element and delete the resulting window.

A floating window cannot be closed if it has a child. The number in the title bar indicates if it has a parent. For example, the numbers 1.2, 1.4.1, and 2.3 mean that their parents are 1, 1.4, and 2, respectively.

A child of a floating window is a floating window that contains a definition or theorem related to its parent. For example, if a floating window contains the partial order definition: Definition of: P_ORDER; If RELAT_IN(R,A), then we will say that P_ORDER(R,A) if and only if ANTISYMMETRIC(R,A) AND REFLEXIVE(R,A) AND TRANSITIVE(R,A) and you want to see the definition of REFLEXIVE, just select it, hover "consults" in the main menu, and click "The selected name". The REFLEXIVE definition will appear in a new floating window that is a child of the one with the P_ORDER definition.

Except for the limitations of their screen sizes, the Mathdialog GUI works with touch screen devices such as tablets or mobile phones. Mathdialog.com has been tested with Firefox, Chrome, Opera, and Edge. However, it does not work on Mac computers, tablets, or phones.

Mathdialog.com has been tested with Firefox, Chrome, Opera, and Edge web browsers.

The website mathdialog.com is just the user interface; the red button means the browser cannot connect to the Mathdialog program. There are many reasons for this, but it should be temporary, at most 5 minutes. If it takes longer, a serious problem is occurring. It also happens with incompatible browsers.